Fungsi, dalam istilah matematika adalah pemetaan setiap anggota sebuah himpunan (dinamakan sebagai domain) kepada anggota himpunanyang lain (dinamakan sebagai kodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
Ringkasan Materi
A. Relasi
Aturan yang menghubungkan setiap anggota himpunan A ke B disebut Relasi dari A ke B.
Di tulis : R : A→B.
Istilah-istilah :
Himpunan A disebut Domain = Daerah Asal
Himpunan B disebut Kodomain = Daerah Kawan
Range = Daerah Hasil
B. Menyatakan Relasi
Relasi dapat dinyatakan dengan tiga cara, yaitu :
1. Diagram Panah
2. Himpunan Pasangan Berurutan
3. Grafik Cartesius
C. Produk Cartesius
Jika x ϵ A dan y ϵ B, maka produk Cartesius A ke B adalah himpunan pasangan berurutan (x, y).
Ditulis : AxB ={(x, y)І xϵ A dan yϵ B}
Contoh :
A = {a, b, c}
B = {1, 2}
maka dengan menggunakan tabel A x B di peroleh :
A x B
|
1
|
2
|
a
|
(a, 1)
|
(a, 2)
|
b
|
(b, 1)
|
(b, 2)
|
c
|
(c, 1)
|
(c, 2)
|
A x B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}
Sifat-sifat :
1. A x B ≠ B x A
2. n(A x B) = n(B x A)
D. Pemetaan (Fungsi)
Pemetaan adalah relasi khusus yang memasangkan setiap anggota himpunan A dengan tepat pada satu anggota himpunan B.
Pemetaan adalah relasi khusus yang memasangkan setiap anggota himpunan A dengan tepat pada satu anggota himpunan B.
Komposisi Fungsi
Komposisi fungsi merupakan penggabungan operasi dua fungsi secara berurutan yang akan menghasilkan sebuah fungsi baru.
Komposisi dua fungsi  dan
dan 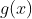 dinotasikan dengan simbol
dinotasikan dengan simbol 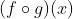 atau
atau 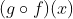 .
.
dimana
Sifat Komposisi Fungsi
Contoh :
diberikan fungsi :
1. 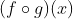 = ….?
= ….?
* fungsi 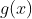 disubtitusikan ke fungsi
disubtitusikan ke fungsi 
2. 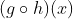 = ….?
= ….?
* fungsi 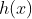 disubtitusikan ke fungsi
disubtitusikan ke fungsi 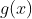
3.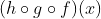 =…?
=…?
* fungsi  disubtitusikan terlebih dahulu ke fungsi
disubtitusikan terlebih dahulu ke fungsi 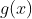 nah, hasilnya baru disubtitusikan ke fungsi
nah, hasilnya baru disubtitusikan ke fungsi 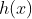 , perhatikan warna mewakili subtitusi ….ok!
, perhatikan warna mewakili subtitusi ….ok!
Bagaimana contoh diatas???sudah cukup jelas,kan???!!
Berhati-hatilah dalam mensubtitusikan ya….
Berhati-hatilah dalam mensubtitusikan ya….
Mencari salah satu fungsi jika komposisi fungsi diketahui
1. Mencari 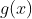 jika
jika  dan
dan 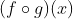 diketahui
diketahui
contoh soal dan pembahasan :
Diketahui 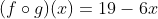 dan
dan 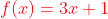 tentukan fungsi
tentukan fungsi 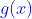 !
!
jawab :
2. Mencari  jika
jika 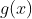 dan
dan 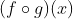 diketahui
diketahui
contoh soal dan pembahasan :
Diketahui 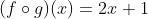 dan
dan 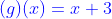 tentukan
tentukan 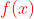 !
!
jawab :
Kita misalkan dulu :
Subtitusikan kembali ke fungsi :
****
Tag :
Education

2 Komentar untuk "Materi SMA : Fungsi (Relasi) Matematika"
Sangat bermanfaat bagi yang lagi belajar.
Tapi jujur aja ane puyeng banget waktu jaman dulu sekolah sama yang namanya MAT, apalagi FISIKA, mending pelajaran afalan deh. Hahaha
setuju.. kalau saya sendiri lebih menyukai pelajaran fisika..hehe
Komentarlah Dengan Baik dan Benar. Jangan ada SPAM dan beri kritik saran kepada blog ILMU DUNIA DAN AKHIRAT.
Mengingat Semakin Banyak Komentar SPAM maka setiap komentar akan di seleksi. :)
"Barangsiapa beriman kepada Allah dan hari akhir hendaklah berbicara yang baik-baik atau diam." (HR. Bukhari)
>TERIMA KASIH<