Assalamu'alaikum..
Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan | Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan itu yang saya anggap sulit di pelajaran matematika. bukan hanya trifono metri, tapi aljabar pula. Taoi bukan berarti saya tak akan memberikan Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan ini kepada kalian looo | hal ini di sebabkan sekarang ini, kalo guru tak bisa, tanya mbah google. apa lagi mengenai Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan yang agak susah. hadeeh...
Belajar matematika tu ga kayak membalikkan telapak tangan looo. Butuh proses yang panjang and rumit. Udah de, mangg di lihat Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan
Tapi lihat pula ya Keanehan di Jalur Gaza dan Mengapa blog ini di sebut blog ILMU DUNIA DAN AKHIRAT??
=( 1/ cot x + 1/ coty ) / ( 1- 1/ cotx coty)
= ( cotx + coty ) / cotx coty / ( cotx coty - 1)/ cotx coty
= ( cotx+coty)/(cotx*coty-1)
Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan | Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan itu yang saya anggap sulit di pelajaran matematika. bukan hanya trifono metri, tapi aljabar pula. Taoi bukan berarti saya tak akan memberikan Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan ini kepada kalian looo | hal ini di sebabkan sekarang ini, kalo guru tak bisa, tanya mbah google. apa lagi mengenai Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan yang agak susah. hadeeh...
Belajar matematika tu ga kayak membalikkan telapak tangan looo. Butuh proses yang panjang and rumit. Udah de, mangg di lihat Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan
Tapi lihat pula ya Keanehan di Jalur Gaza dan Mengapa blog ini di sebut blog ILMU DUNIA DAN AKHIRAT??
How to solve tan(x+ y) = (tan x + tan y) / (1 - tan x tan y)?
sin(x+y) = sinx cosy + cosx siny
cos(x+y) = cosx cosy - sinx siny
tan(x+y) = [sinx cosy + cosx siny] / [cosx cosy - sinx siny]
cos(x+y) = cosx cosy - sinx siny
tan(x+y) = [sinx cosy + cosx siny] / [cosx cosy - sinx siny]
Question :
(tanx+tany)/(1-tanx*tany) = (cotx+coty)/(cotx*coty-1)
Answer :
A=(tanx +tany ) / (1-tanxtany)
A=( 1/cotx + 1/coty) / (1- 1/cotx coty)
A= ((coty +cotx)/cotxcoty ) / (cotxcoty -1) /cotxcoty
A= ((cotx +coty ) / cotxcoty) * (cotxcoty /(cotxcty-1)
A= (cotx +coty) / (cotxcoty -1)
A=( 1/cotx + 1/coty) / (1- 1/cotx coty)
A= ((coty +cotx)/cotxcoty ) / (cotxcoty -1) /cotxcoty
A= ((cotx +coty ) / cotxcoty) * (cotxcoty /(cotxcty-1)
A= (cotx +coty) / (cotxcoty -1)
Or
=( 1/ cot x + 1/ coty ) / ( 1- 1/ cotx coty)
= ( cotx + coty ) / cotx coty / ( cotx coty - 1)/ cotx coty
= ( cotx+coty)/(cotx*coty-1)
sin(-x) = -sin(x) csc(-x) = -csc(x) cos(-x) = cos(x) sec(-x) = sec(x) tan(-x) = -tan(x) cot(-x) = -cot(x)
tan(x 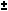 y) = (tan x y) = (tan x 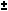 tan y) / (1 tan y) / (1 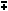 tan x tan y) tan x tan y)sin(2x) = 2 sin x cos x cos(2x) = cos^2(x) - sin^2(x) = 2 cos^2(x) - 1 = 1 - 2 sin^2(x) tan(2x) = 2 tan(x) / (1 - tan^2(x)) sin^2(x) = 1/2 - 1/2 cos(2x) cos^2(x) = 1/2 + 1/2 cos(2x) sin x - sin y = 2 sin( (x - y)/2 ) cos( (x + y)/2 ) cos x - cos y = -2 sin( (x - y)/2 ) sin( (x + y)/2 )
Given Triangle abc, with angles A,B,C; a is opposite to A, b opposite B, c opposite C: a/sin(A) = b/sin(B) = c/sin(C) (Law of Sines)
(a - b)/(a + b) = tan [(A-B)/2] / tan [(A+B)/2] (Law of Tangents) | |||||||||||||||||||||||||||||||||||||||||||||||
Soal Latihan :
1. tan (x+y) / cos x cos y = tan x + tan y
2. sin (x-y) / tan x - tan y = cos x cos y
3. sin (x+y) . sin (x-y) = sin^2 x - sin^2 y
4. sin(x+y) - sin(x-y) / cos (x+y) + cos (x-y) = tan y
5. BC=CD=1 satuan. Gunakan rumus sin (A+B) untuk menunjukkan bahwa V3 sin a + cos a = 4 / V7
2. sin (x-y) / tan x - tan y = cos x cos y
3. sin (x+y) . sin (x-y) = sin^2 x - sin^2 y
4. sin(x+y) - sin(x-y) / cos (x+y) + cos (x-y) = tan y
5. BC=CD=1 satuan. Gunakan rumus sin (A+B) untuk menunjukkan bahwa V3 sin a + cos a = 4 / V7
Soal Latihan 2 :
1. Di ketahui sin x = 1/2, dan x sudut di kuadran pertama, hitunglah :
a. Cos x
b. Tan x
(ket : x = alpa)
~
2. Diketahui cos A = - 4/5 dan A sudut dikuadran ketiga. Hitung :
a. Sin A (aku dapat hasilnya = - akar 9/25)
b. Tan A (aku dapat hasilnya = akar 9/16)
~
3. Jika sin x = 12/13 dan cos y = 24/25 (x dan y masing masing sudut lancip). Hitunglah :
a. Cos x
b. Tan x
c. Sin y
d. Tan y
e. Sin x Cos y - Cos x Sin y
f. Cos x Cos y - Sin x Sin y
g. Tan x + Tan y = 1 - Tan x Tan y
a. Cos x
b. Tan x
(ket : x = alpa)
~
2. Diketahui cos A = - 4/5 dan A sudut dikuadran ketiga. Hitung :
a. Sin A (aku dapat hasilnya = - akar 9/25)
b. Tan A (aku dapat hasilnya = akar 9/16)
~
3. Jika sin x = 12/13 dan cos y = 24/25 (x dan y masing masing sudut lancip). Hitunglah :
a. Cos x
b. Tan x
c. Sin y
d. Tan y
e. Sin x Cos y - Cos x Sin y
f. Cos x Cos y - Sin x Sin y
g. Tan x + Tan y = 1 - Tan x Tan y
Pembahasan :
1.] sin x = 1/2 , x = 30°
a.) cos x = cos 30 = (1/2)√3
b.) tan x = tan 30 = (1/3)√3
2.] cos A = -4/5 , A = 217°
a.) sin A = sin 217 = -3/5
b.) tan A = tan 217 = 3/4
3.] sin x = 12/13 , cos y = 24/25, gunakan aturan segitiga siku-siku
a.) cos x = 5/13
b.) tan x = 12/5
c.) sin y = 7/25
d.) tan y = 7/24
e.) = sin x cos y - cos x sin y
= (12 . 24) / (13 . 25) - (5 . 7) (13 . 25)
selesaikan sendiri yaa
f.) = cos x cos y - sin x sin y
= (5 . 24) / (13 . 25) - (12 . 7) / (13 . 25)
selesaikan sendiri yaa
e.) tan x + tan y = 1 - tan x tan y
= tan (x + y)
a.) cos x = cos 30 = (1/2)√3
b.) tan x = tan 30 = (1/3)√3
2.] cos A = -4/5 , A = 217°
a.) sin A = sin 217 = -3/5
b.) tan A = tan 217 = 3/4
3.] sin x = 12/13 , cos y = 24/25, gunakan aturan segitiga siku-siku
a.) cos x = 5/13
b.) tan x = 12/5
c.) sin y = 7/25
d.) tan y = 7/24
e.) = sin x cos y - cos x sin y
= (12 . 24) / (13 . 25) - (5 . 7) (13 . 25)
selesaikan sendiri yaa
f.) = cos x cos y - sin x sin y
= (5 . 24) / (13 . 25) - (12 . 7) / (13 . 25)
selesaikan sendiri yaa
e.) tan x + tan y = 1 - tan x tan y
= tan (x + y)
Soal Latihan 3 :
Jika tan x + tan y = 25 dan cot x + cot y = 30, maka nilai tan (x + y) adalah
Rumus trigonometri umum

yang ini sering juga keluar di soal snmptn
Sudut-Sudut Istimewa sin cos tan 0 30 45 60 90 derajat
Aturan sin cos tan lain
Rumus-rumus Trigonometri pada segitiga dengan sisi a b c
Aturan sinusRumus jumlah 2 sudut trigonometri sin cos tan
Aturan Cosinus
Luas Segitiga 2 sisi dan 1 sudut
Luas segitiga dengan 3 sisi akan dibahas lain waktu
Sudut 2A atau sin 2x, cos 2x, tan 2x
sepertinya gambar ini ada yang salah, nanti diperbaiki
Rumus kali trigonometri sin cos cos sin cos cos -sin sin
Rumus jumlah 2 trigonometri sin cos cos sin cos cos -sin sin
Persamaan Trigonometri mudah sekali dikerjakan
Bentuk a Cos x + b Sin x = k cos x-teta
Bentuk a Cos x + b Sin x = c
Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x

yang ini sering juga keluar di soal snmptn
Fungsi dasar:
Rumus setengah sudut



Rumus sudut rangkap dua

Penjumlahan
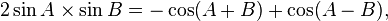
Identitas trigonometri

Semoga bisa membantu kalian Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan ini.. :)
Wassalamu'alaikum...








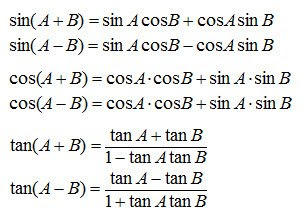






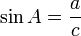

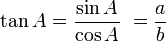
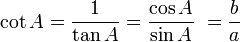

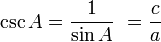



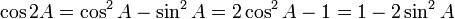
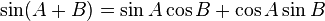
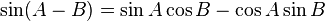
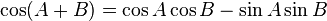

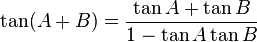
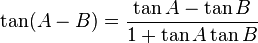




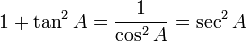

19 Komentar untuk "Kumpulan Rumus Trigonometri dan Harga Sin Cos Tan"
Terima kasih atas rumusnya.. Mantab infonya..
Thanks gan buat rumusnya. Btw trigono itu susahnya meres otak wkwk xD
makasih infonya
terima kasih. semoga kebaikan Anda dibalas Allah
Aamiin
makasih sudah mw berkunjung ke mari gan
sama sama gan
hahaha
bner, aku aja sampai saat ini amsih pusing ama trigono :3
hahaha
maaf gan :D
emank mtk gtu
Makasih infony, sangat membantu sekali, apalagi buat yg udh lama meninggalkan trigono, jd bsa ingat lg,,,hehe
Makasih banyaaaaaaaaaaaakkkk <3
sangat bermanfaat kak.. terimakasih kak...
Susah XD
sin x cos x
-------------------- sama dengan berapa gan ? pliss jawab cepet y gan :3 lagi butuh buat bsok
tan x
a
a
sin x cos x
--------------------- sama dg breapa gan? pliss jwab cepet y gan.. aku butuh banget buat besok
tan x
F(x)=2sin 2x
Itu gmana?buat bwsok gan
thanks kak atas infonya benar2 bermanfaat., :)
thanks kak atas infonya benar2 bermanfaat., :)
Komentarlah Dengan Baik dan Benar. Jangan ada SPAM dan beri kritik saran kepada blog ILMU DUNIA DAN AKHIRAT.
Mengingat Semakin Banyak Komentar SPAM maka setiap komentar akan di seleksi. :)
"Barangsiapa beriman kepada Allah dan hari akhir hendaklah berbicara yang baik-baik atau diam." (HR. Bukhari)
>TERIMA KASIH<